本篇筆記整理 CVPR 2023 的 Humans in Minutes,聚焦在單眼影片中以數分鐘完成可自由視角的動態人體重建。方法以 SMPL 為骨架先驗,將 4D 體積運動重參數化為 2D 表面 UV 與時間,並結合 inverse LBS 與殘差形變在 canonical space 學習位姿變形;同時採用依部位切分的 part-based voxelized 表示與多解析度 hash encoding,依人體區塊複雜度高效建模密度與顏色。相較既有 NeRF 類方法,本作在維持競爭力的畫質下,將優化時間縮短至百倍等級(512×512、RTX 3090 約數分鐘),訓練僅需每幀姿態與前景遮罩,並於文中進一步分析損失設計、正則化與對 SMPL 依賴等限制。
論文資訊
- Link: https://arxiv.org/abs/2302.12237
- Conference: CVPR 2023
Introduction#
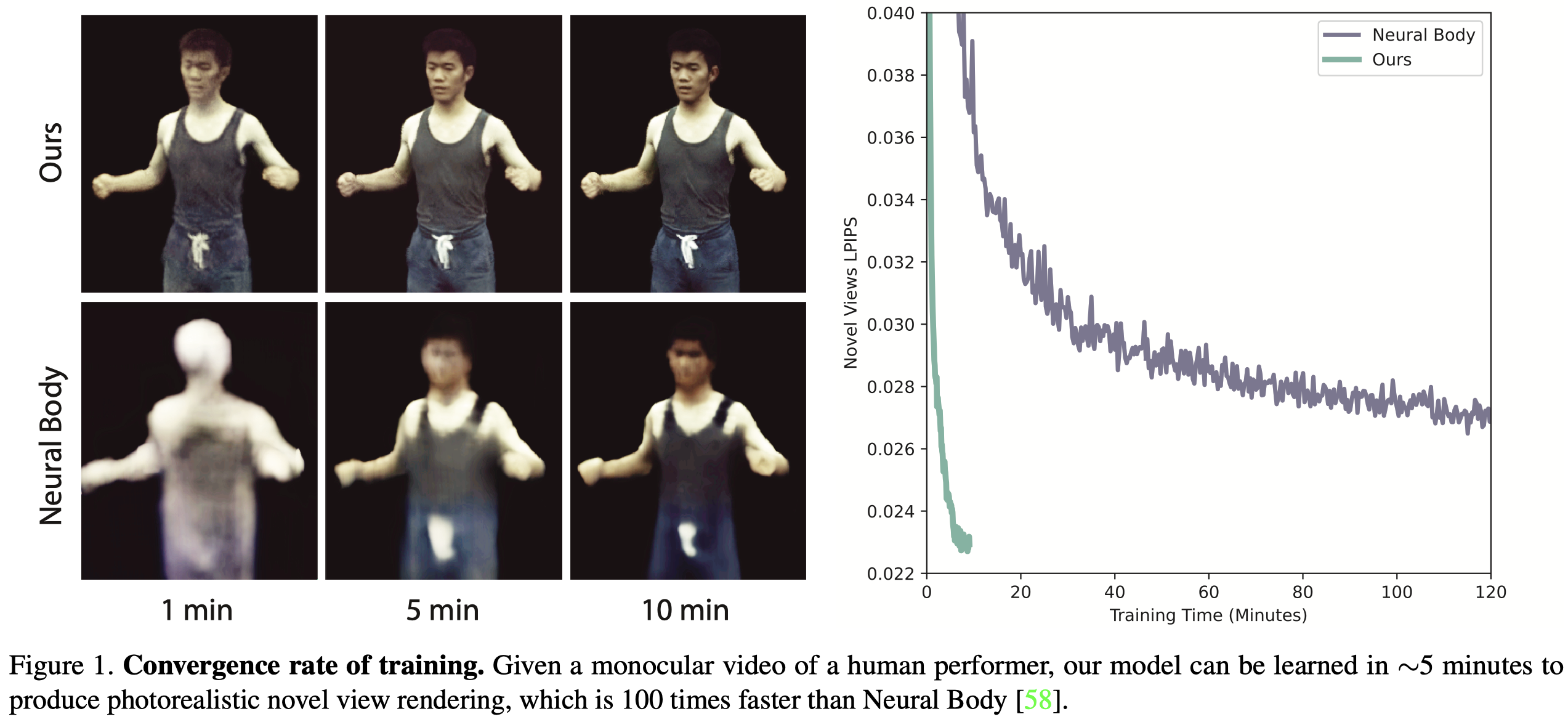
- Topic:Accelerate 3D human reconstruction。
- Previous works:Neural Body, HumanNeRF, etc.
- Problems:訓練時間很長,約十小時。
- Contributions
- 提出一種 part-based voxelized human representation,可以實現高效建模。
- 通過 2D motion parameterization scheme,實現更高效的 deformation field modeling。
- 與以往的 neural human representations 相比,保有具競爭力的渲染品質,同時優化速度提高 100 倍。 ($512 \times 512$ resolution on an RTX 3090 GPU)
Methods#
Overview#
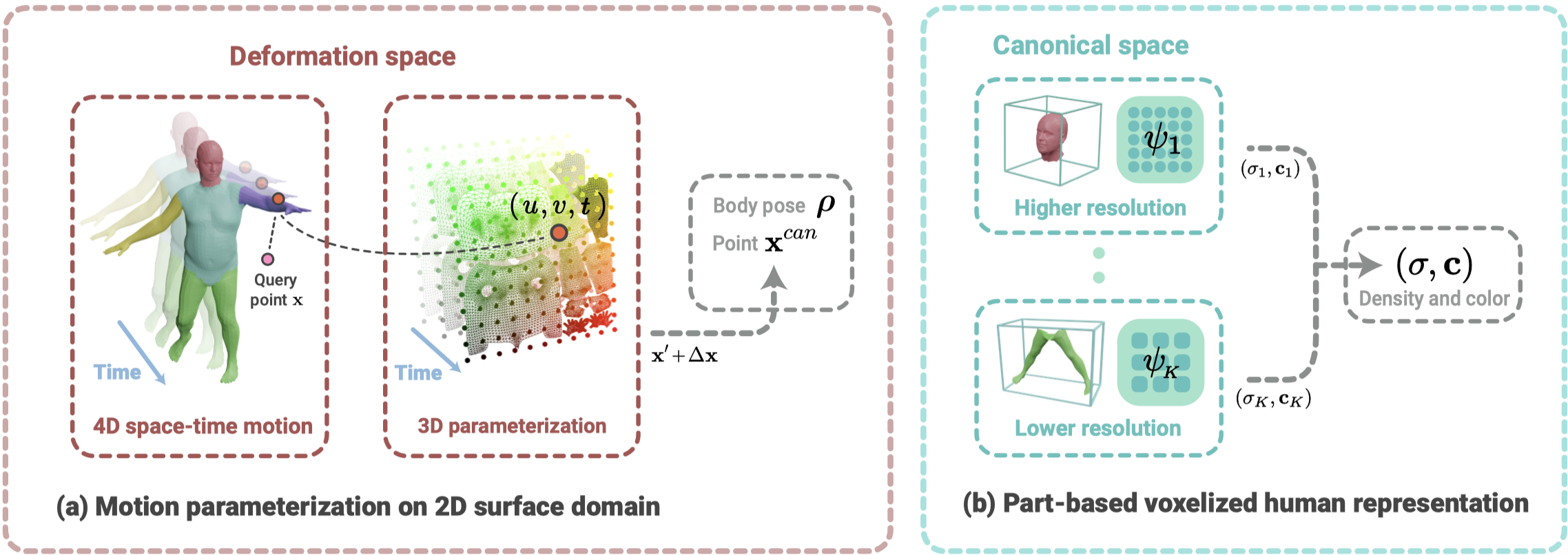

- 本篇方法需要提供每個圖像的 human pose 與 foreground human mask。
(a) 將 4D 的場景表示,通過 prior 降維成 3D,接著通過 inverse LBS module 和 residual deformation module 將 observed pose 轉換成 canonical pose。
(b) 在 canonical space 中,將人體按照 SMPL 的基礎切割成不同部位,並通過 Instant-NGP 的 Multi-resolution Hash Encoding 為不同部位進行建模。最後將結果通過 argmax 合併,生成最終的 $(\sigma, \mathbf{c})$。
Proposed human representation#
Motion parameterization on 2D surface domain#
- 對於要 query 的點 $\mathbf{x}$,首先找到他在 SMPL 上最近的 surface point p,接著通過 Neural Actor 中的作法得到 blend weight w 與 UV coordinate (u, v)。
- 通過 motion field 將 query point x 映射到 canonical space 相對應的點 $\mathbf{x}^{\text{can}}$。
- Motion field 由 inverse LBS module 和 residual deformation module 組成。
Inverse LBS module
$$ \begin{align*} \Phi_{\text{LBS}}(\mathbf{x}, \mathbf{w}, \rho) = \left( \sum_{j=1}^{J} w_{k,j} G_{j} \right)^{-1} \mathbf{x}, \end{align*} \tag{1} $$符號 描述 $\mathbf{x}$ The query point $\mathbf{w}$ The blend weight $\rho$ The human pose $G_j$ The transformation matrices derived form $\rho$ - 給定 query point x、blend weight w 與 pose $\rho$,可以將其轉換到 unposed space。
Residual deformation module
$$ \begin{align*} \Delta \Phi(u, v, t) = \text{MLP}_{\text{res}}\!\left( \psi_{\text{res}}(u, v, t) \right), \end{align*}\tag{2} $$符號 描述 $\psi_{\text{res}}$ The multiresolution hash encoding $t$ The latent code of time - 作者觀察到典型的人體動作通常發生在 surface level 而非 volumetric level。因此 UV coordinate 中相近的座標會有相似的運動。
- 透過這樣的先驗,可以將訓練所需的 4D volumetric motion 降維成 3D surface-time domain,進而加速訓練。$(x,y,z,t) \rightarrow (u,v,t)$
完整的 Motion field 如 Eq.\ref{eq:3} 所示:
$$ \begin{align*} \mathbf{x}^{\text{can}}(\mathbf{x}, \mathbf{w}, u, v, \rho, t) = \Phi_{\text{LBS}}(\mathbf{x}, \mathbf{w}, \rho) + \Delta \Phi(u, v, t). \end{align*}\tag{3} \label{eq:3} $$
Part-based voxelized human representation#
雖然引入 Multiresolution Hash Encoding,但作者認為,人體每個部位複雜度不同,因此針對每個人體部位,應該調整適當的 resolution。
作者利用 SMPL 中的 blend weight 來分解 SMPL template mesh $\mathcal{M} = (\mathcal{V}, \mathcal{E})$。其中 $\mathcal{V}$ 為頂點,$\mathcal{E}$ 為邊界。
對於 $i$-th 頂點 $v_i$ 具有 blend weight $w_i$,並且對於每個部位 $k$,作者定義 $\Omega_k$ 作為屬於這個部位的 set of bones 。
The mesh of the $k$-th part is defined as $\mathcal{M}_k = (\mathcal{V}_k, \mathcal{E}_k)$。
$$ \begin{align*} \mathcal{V}_{k} &= \{ v_i \mid \text{argmax}\ w_i \in \Omega_k \}, \tag{4} \\ \mathcal{E}_{k} &= \{ (v_i, v_j) \mid v_i \in \mathcal{V}_k, \, v_j \in \mathcal{V}_k \}. \tag{5} \end{align*} $$
給定轉換後的點,同樣對其進行 hash encoding ,並計算 density 與 color。這邊要注意的是,作者已經提前為每個 part 定義了相關 hash encoding function 的參數。
Density
$$ \begin{align*} (\sigma_k, \mathbf{z}) = \text{MLP}_{\sigma_k}\!\left( \psi_k(\mathbf{x}) \right), \end{align*}\tag{6} $$- 除了預測 density,同時預測了一個 feature vector $\mathbf{z}$。
- Note: 這邊的 $\mathbf{x}$ 並非 observed space 中的 query point,而是經過 motion field 轉換後的 transformed point (canonical point)。
Color
$$ \begin{align*} \mathbf{c}_k = \text{MLP}_{\mathbf{c}_k}\!\left( \mathbf{z}, \mathbf{d}, \ell_t \right). \end{align*}\tag{7} $$符號 描述 $\mathbf{d}$ The viewing direction $\ell_t$ The latent embedding for each video frame $t$
由於有 $K$ 個 part,因此最終會得到 $K$ 個預測結果 $\{(\sigma_k, \mathbf{c}_k)\}^K_{k=1}$,並透過 Eq.\ref{eq:8} 計算得到最終的 density 與 color。也就是以該點具有最大 density 的 color 作為最終的 color。
$$ \begin{align*} (\sigma, \mathbf{c}) = (\sigma_{k^*}, \mathbf{c}_{k^*}), \quad \text{where } k^* = \arg\max_{k} \sigma_k. \end{align*}\tag{8} \label{eq:8} $$
Experiments#
Training#
Loss Function
$$ \begin{align*} L_{\text{rgb}} = \left\lVert \tilde{I}_{P} - I_{P} \right\rVert_{2} + \left\lVert F_{\text{vgg}}(\tilde{I}_{P}) - F_{\text{vgg}}(I_{P}) \right\rVert_{2}, \end{align*}\tag{9} $$- MSE Loss
- Perceptual loss
Regularizer
- 使用 Mip-NeRF 360 中的正則化器,用來使 density 集中在人體表面。
- 約束 residual deformation field 表現的小與平滑。
Implementation details#
- 設備:單張 3090。
- 框架:以 PyTorch 實現,以與其他 baseline 比較。
Experiment Setting#
- Datasets
- ZJU-MoCap
- MonoCap: 來自 DeepCap 和 DynaCap dataset,包含四個場景。
- Metrics
- PSNR, SSIM, LPIPS
Comparison#
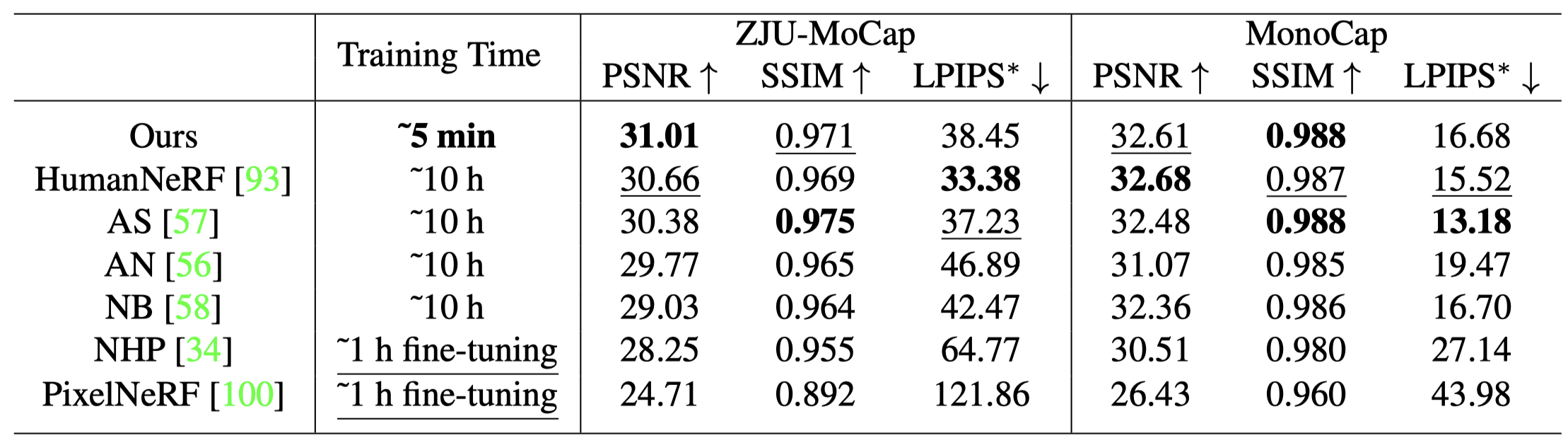
- ZJU-MoCap
- 本篇方法僅需 5 mins 的訓練時間,而其他的方法需要大於 10 hrs 的時間,甚至 NHP 與 PixelNeRF 需要先 pretrain 10 hrs 再 finetune 1 hr。
- 本篇方法在三個指標上都呈現了可比較性的渲染品質。
- MonoCap
- 本篇同樣表現出有競爭力的結果。

- ZJU-MoCap
- Monocular 的設置下,Generalizable 的方法無法很好的渲染正確的人體形狀。
- MonoCap
- 本篇方法可以產生不錯的細節。
- HumanNeRF 與 AS 雖然可以生成很好的結果,但時間開銷會是本篇的 100 倍。
Ablation Studies#
Ablation Studies on Proposed Components#
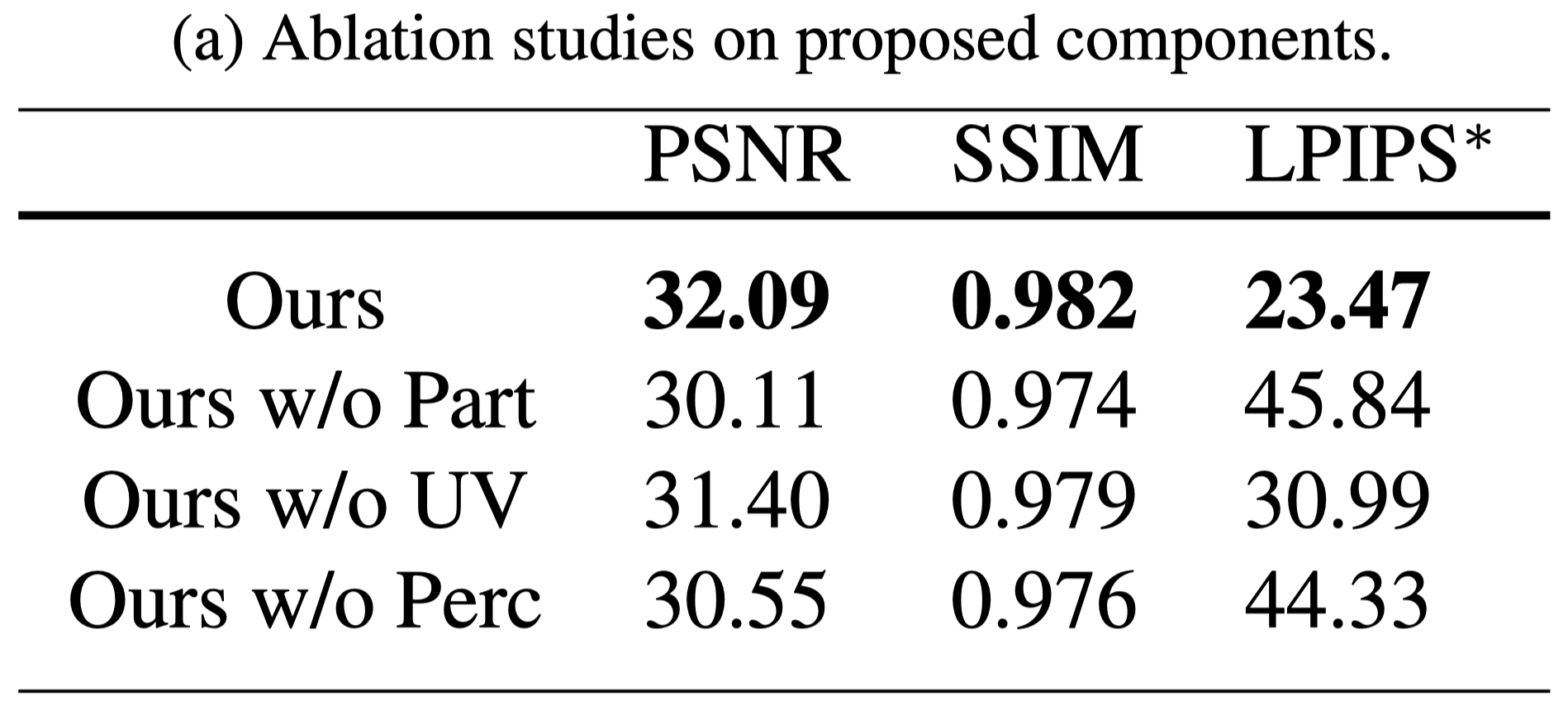
- 當沒有 part-based human representation,效果顯著下降。
- 當 $\text{MLP}_{\text{res}}$ 改以經過 hash encode 的 $(\text{x}, t)$ 作為輸入,表現出較差的效果。因為嚴重的 hash collision 與解析度不足。
- 移除 perceptual loss 之後,LPIPS 分數明顯變差。
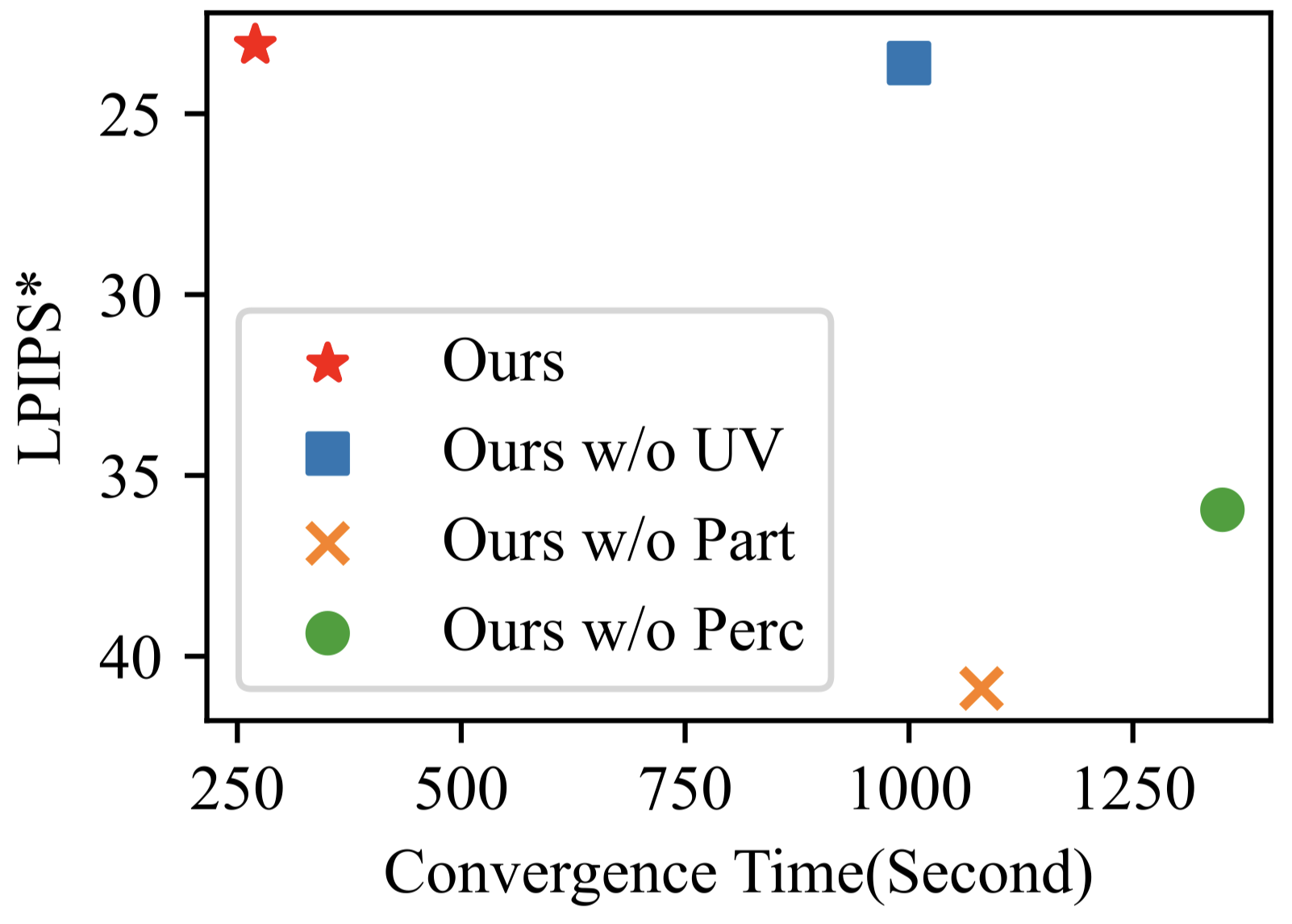
- 當沒有使用 UV coordinate 作為輸入,訓練時間顯著提升。

- 當沒有使用 part-based human representation,渲染結果明顯變差。
Analysis of the part-based voxelized human representation#
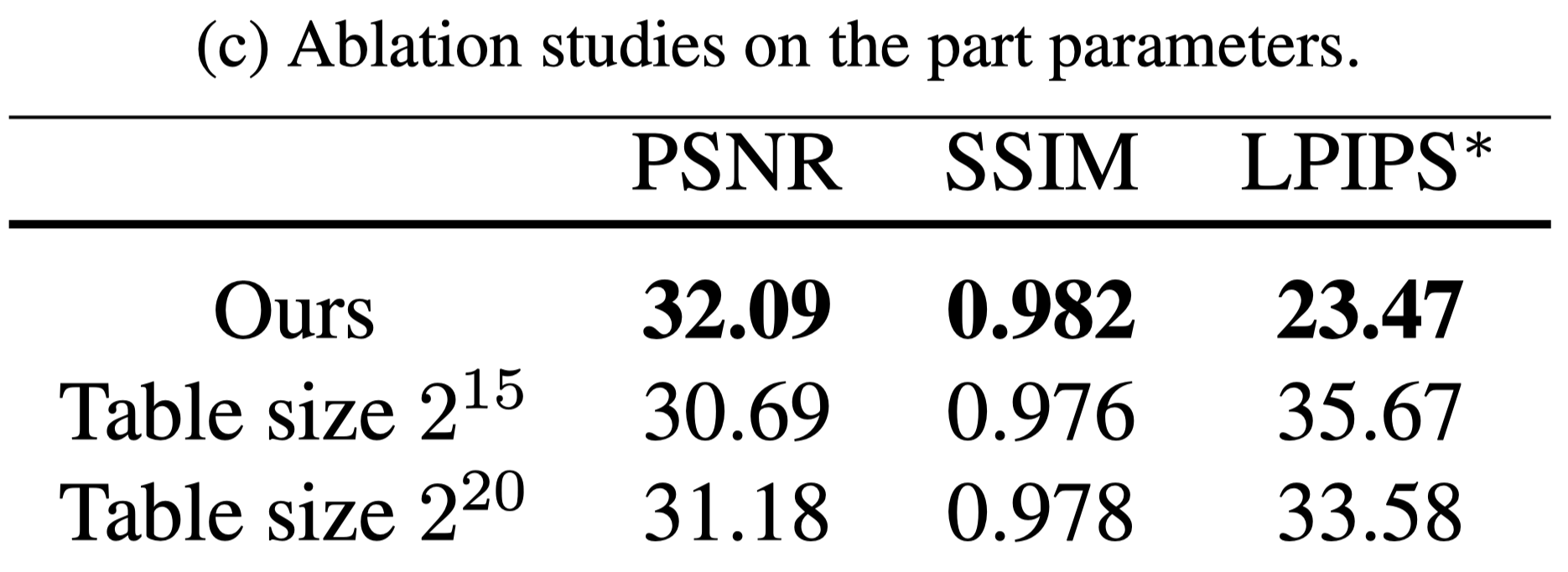
- 單純的增加 hash table 的大小並不能在同樣的時間下帶來更好的表現。因為更大的 hash table 會增加內存開銷與訓練迭代時間。
- 本篇的方法可以基於人體不同部位的複雜度來調整 hash table 的大小,從而有效的表示人體。
Analysis of the motion parameterization scheme#
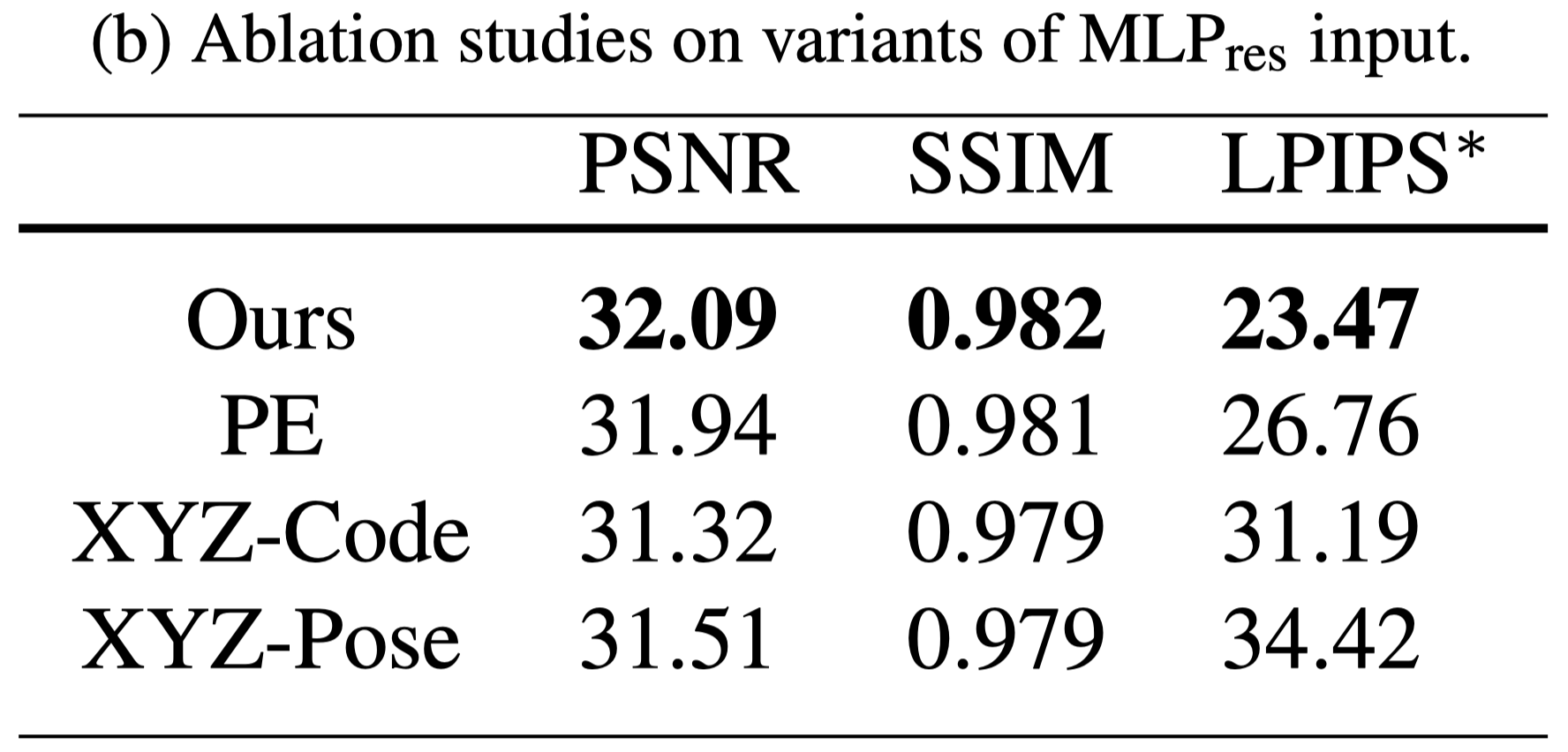
- 在 Tab.2 (a) 中展示過使用 $(x,y,z,t)$ 作為輸入效果並不會比較好,此外會增加記憶體開銷與運算時間。
- 在 Tab.2 (b) 進一步測試不同的 input,仍然可以看到本篇使用的方法效果最好。
Analysis of Robustness#
- 作者在 ZJU-MoCap 的 377 場景上,測試模型的 robustness。(五次 PSNR 達到 30)
- 平均訓練時間 76.00s,標準差為 13.56s。
Conclusion#
Introduce a novel dynamic human representation that can be quickly optimized from videos and used for generating free-viewpoint videos of the human performer
- The motion field reparameterizes the point coordinate as 2D surface-level UV coordinate
- The part-based voxelized human model decomposes the human body into multiple parts and represents each part with an MHE-augmented NeRF network
- The proposed representation can be optimized at 1/100 of the time of previous methods
Limitations
- Rely on SMPL parameters
- Can only reconstruct foreground dynamic humans
