針對自由/任意相机軌跡於大型無界場景的重建與渲染,F2‑NeRF(CVPR 2023)提出以可見相機投影建構的 perspective warping,搭配多重雜湊網格與視角一致採樣,並用 octree 自適應分配前景/背景網格,配合 disparity 與 TV 正則抑制偽影;在 LLFF、NeRF‑360‑V2、Free dataset 展現高速訓練與高品質重建。
論文資訊
- Link: https://arxiv.org/abs/2303.15951
- Conference: CVPR 2023
Introduction#
Topic: 允許使用任意相機軌跡進行訓練與推論。
Previous works:
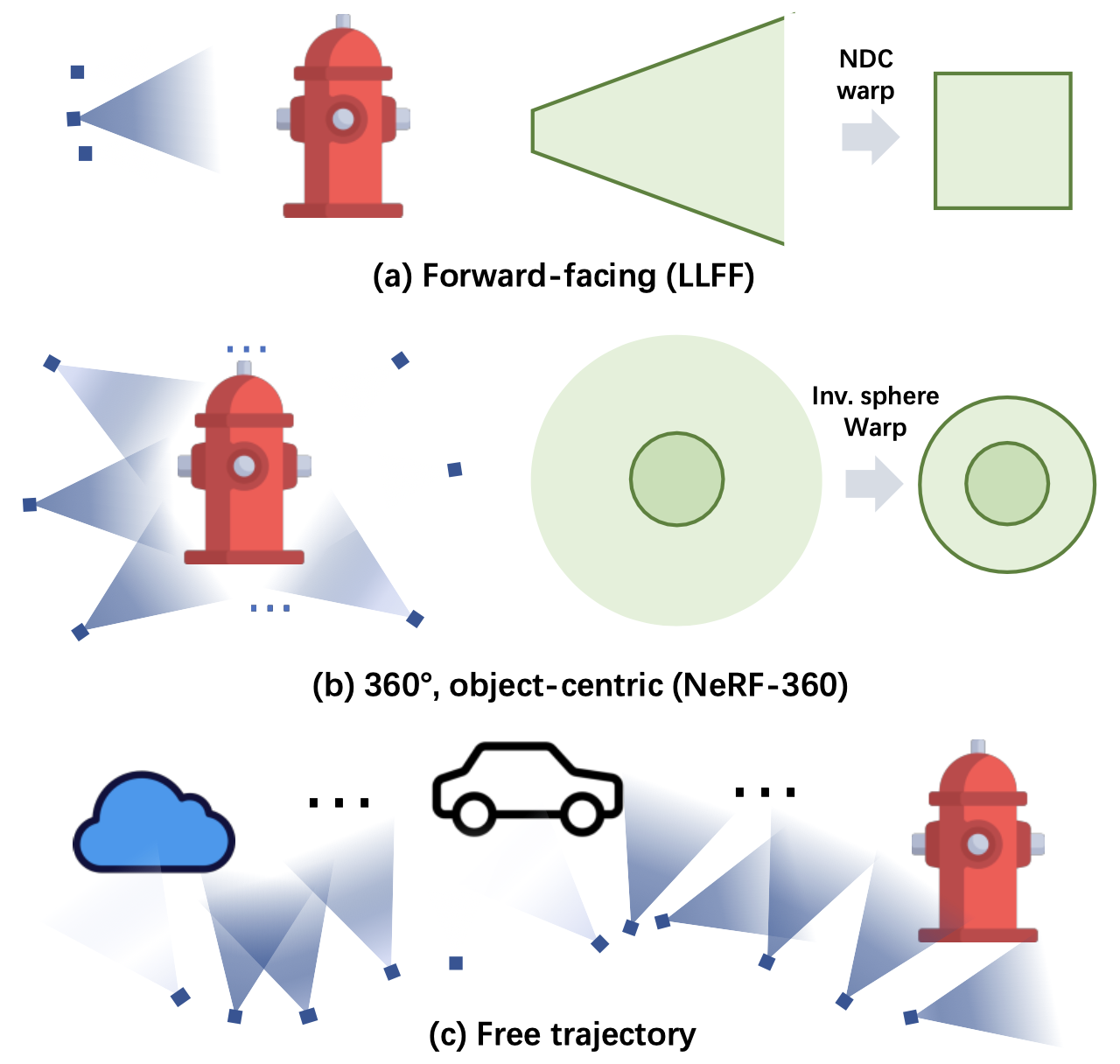
- 為了表示無界場景,常見的策略是使用將無界空間映射成有界空間的空間扭曲方法
- 前向場景
- $360^{\circ}$ 以物件為中心的無界場景
- 無法處理任意軌跡
- 特別是在軌跡很長且包含多個關注物體時,稱為 free trajectories(自由軌跡),如 Fig. 1 (c) 所示
- 為了表示無界場景,常見的策略是使用將無界空間映射成有界空間的空間扭曲方法
Problems
- 在自由軌跡上效能下降是因為 空間表示容量分配失衡
- 當軌跡細長時,場景中的許多區域對任何輸入視角而言都 是空的且不可見
- 在可見的空間中,多個前景物體由稠密且近距離的輸入視角觀測到,而 背景空間則只被稀疏且遠距的輸入視角覆蓋
- 現有的網格式方法會在空間中平均配置網格,造成表示容量的低效使用
- 在自由軌跡上效能下降是因為 空間表示容量分配失衡
Contribution
- 提出 $\text{F}^2$-NeRF(Fast-Free-NeRF),第一個能夠處理大型無界場景自由相機軌跡的快速 NeRF 訓練方法
- 發展一個稱為 perspective warping 的通用空間扭曲方案,適用於任意相機軌跡
- 提出一個 空間細分演算法,自適應地對背景區域使用粗網格,並對前景區域使用細網格
Methods#
Perspective warping#
2D analysis#
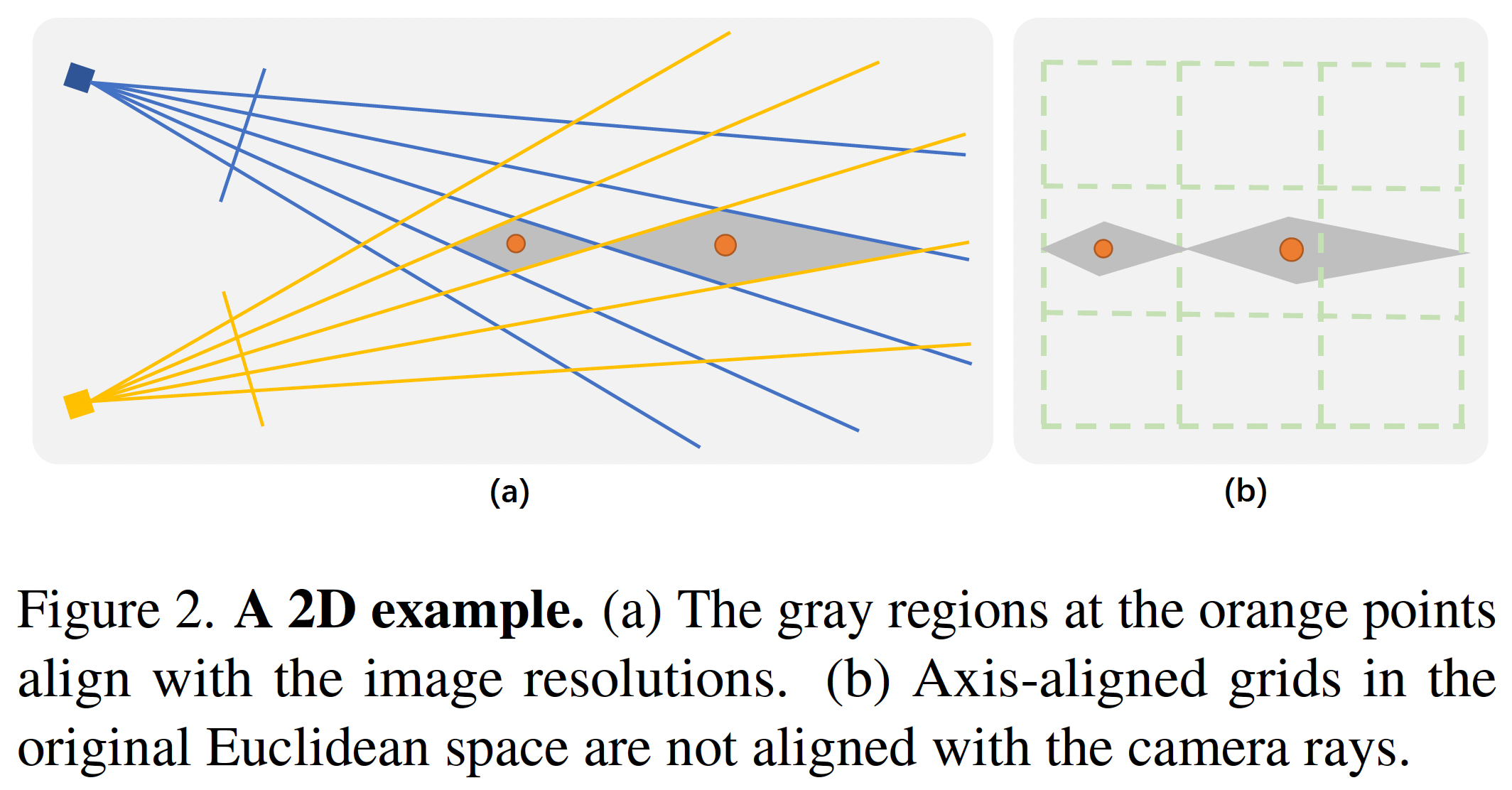
在考慮 2D 情況下,我們需要將 2D 平面上的點投影到兩個 2D cameras 的 1D 座標上。
灰色的菱形是由兩個 camera ray 交會而成,由於相機解析度有限,因此灰色的極為最小的可區分區域。
使用原始的歐式空間對該平面進行分割時,會發現灰色的區域需要由多個 cells 負責,因此浪費計算成本。
因此需要將原始的歐式空間扭曲,使其網格與 camera ray 對齊。
$$ F(\mathbf{x}): \mathbb{R}^2 \rightarrow \mathbb{R}^2 $$$$ F(\mathbf{x}) = F(C_1(\mathbf{x}), C_2(\mathbf{x})) $$符號 描述 $C(\mathbf{x})$ 將 $\text{x}$ 投影到相機上的一維影像座標
3D Definition#
根據在 2D 空間中的推論,作者假設 3D 空間中要有一樣的效果,因此定義 proper warping function 的特性如下。
$$ F: \mathbb{R}^3 \rightarrow \mathbb{R}^3 $$扭曲空間中,兩點之間的距離等於所有可見相機上這兩點之間的距離之和。
$$ \lVert F(\mathbf{x}_1 - F(\mathbf{x}_2) \rVert^2_2 = \sum^n_i \lVert C_i(\mathbf{x}_1) - C_i(\mathbf{x}_2) \rVert^2_2, \text{ where } \mathbf{x}_1, \mathbf{x}_2 \in S $$符號 描述 $S$ The region S in the 3D Euclidean space 扭曲函數是否為 proper 是一個區域性的性質,只與可見的相機有關
3D perspective warping#
實作上,本篇中 $F(\mathbf{x}): \mathbb{R}^3 \rightarrow \mathbb{R}^3$ 是透過下面方式得到。
首先定義一個 observation function ,其會將 3D point 投影到所有相機上。
$$ \mathbf{y} = G(\mathbf{x}) = [C_1(\mathbf{x}), \ldots, C_{n_c}(\mathbf{x})]: \mathbb{R}^3 \rightarrow \mathbb{R}^{2n_c} $$希望找到一個 projection matrix $M \in \mathbb{R}^{3 \times 2n_c}$ ,可以將 $\mathbf{y}_j = G(\mathbf{x}_j) \in \mathbb{R}^{2n_c}$ mapping 至 $\mathbf{z}_j \in \mathbb{R}^3$ 。實際上是使用 PCA 降維。
$$ \mathbf{z}_j = M \mathbf{y}_j $$
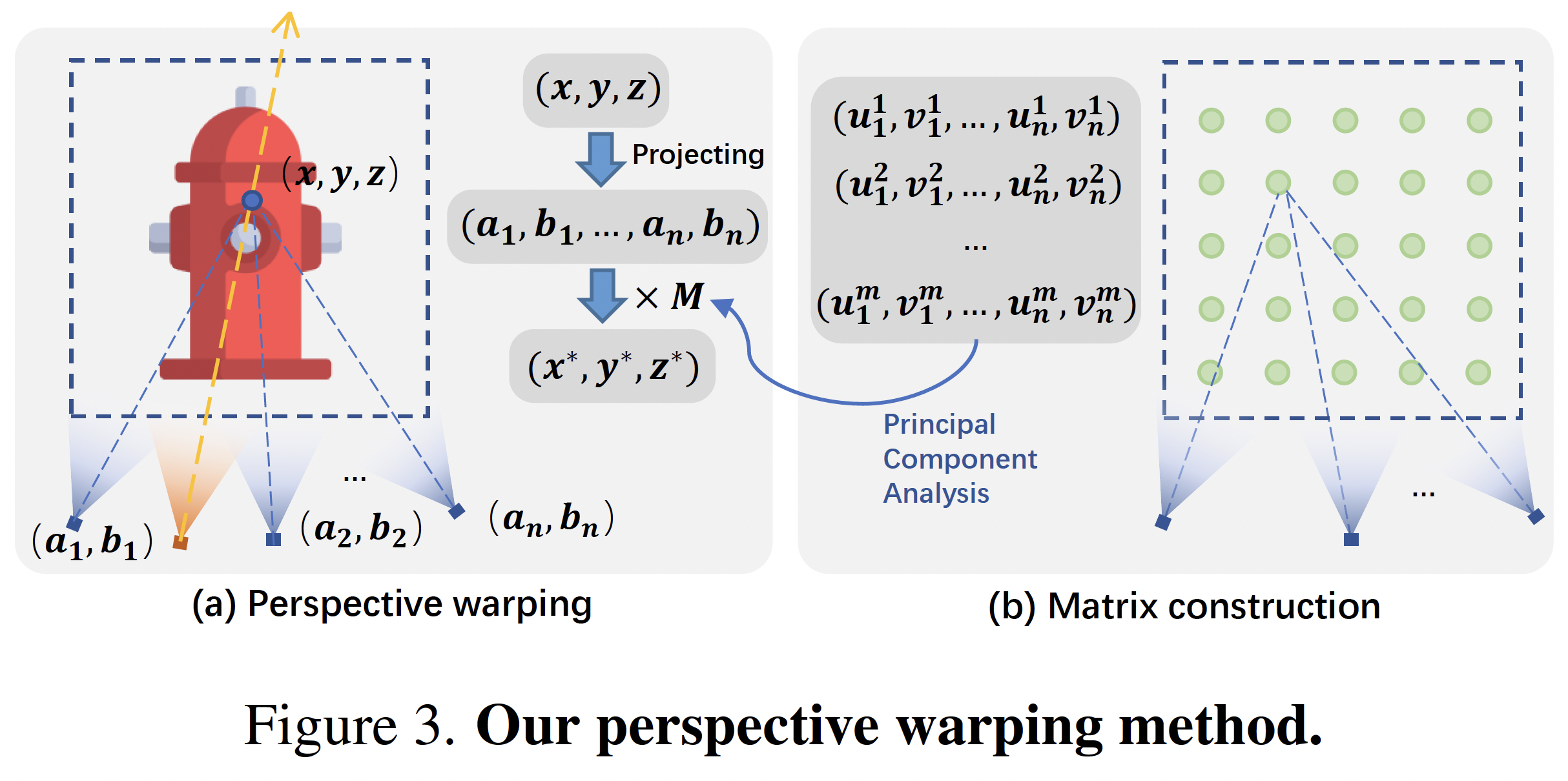
最終表示為
$$ F(\mathbf{x}) = MG(\mathbf{x}) $$Note$M$ projection matrix,實際上為 PCA
Relationship with NDC and inverse sphere warping#
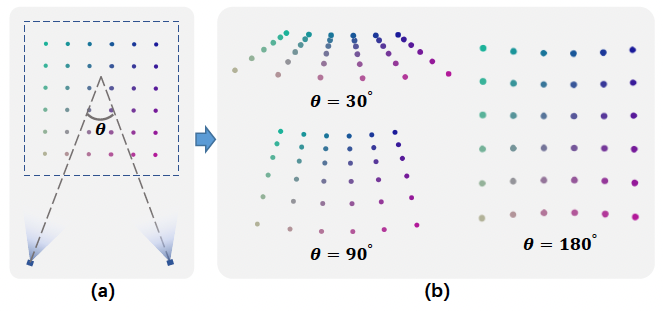
- 當角度較小時:
- 遠處的區域會被壓縮,會近似 NDC warping(前向場景)。
- 當角度較大時:
- 扭曲空間與原始的歐式空間更為相似。
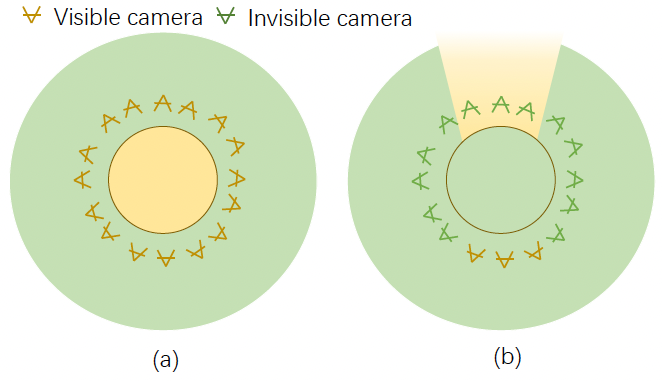
- 對於單位球內部而言,inverse sphere warping 的扭曲空間即為原始的歐式空間,因為周圍所有的相機皆能看到這個單位球
Discussion#
實際上只有兩個相機時,180° 並不會呈現原始歐式空間
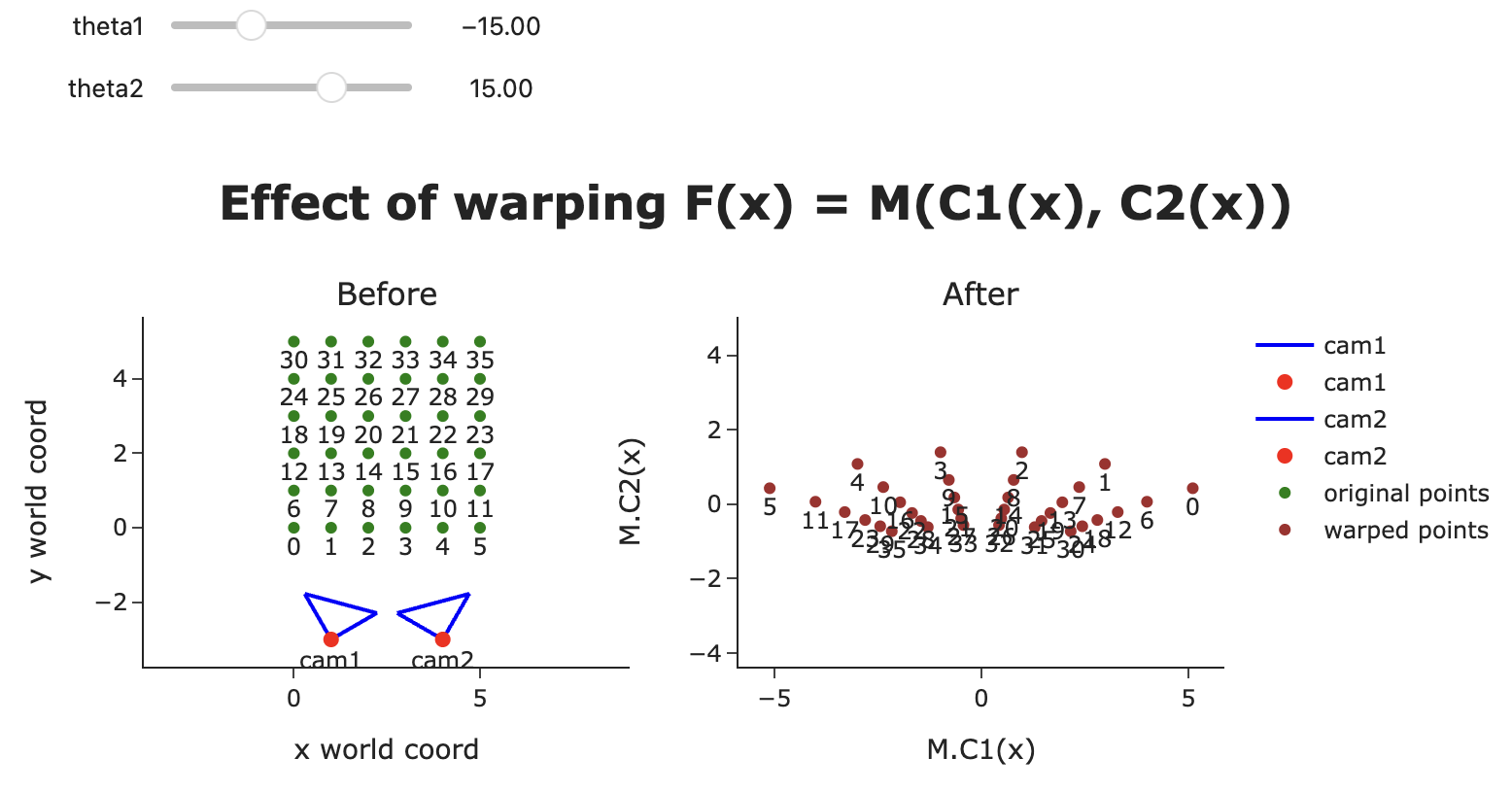
Effect of warping (a). 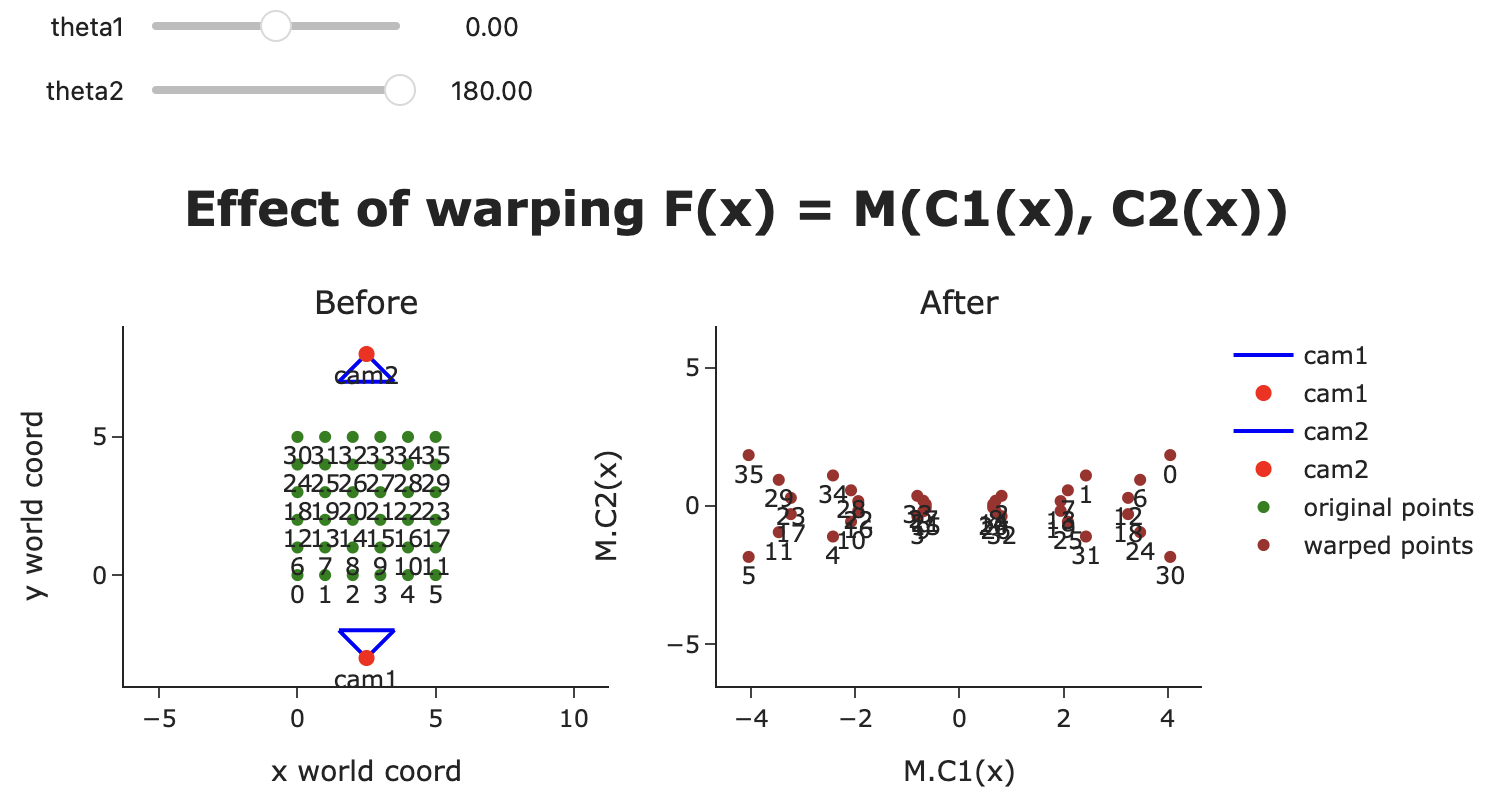
Effect of warping (b). 需要4個以上的相機才能接近歐式空間
Effect of warping (c). 
Effect of warping (d).
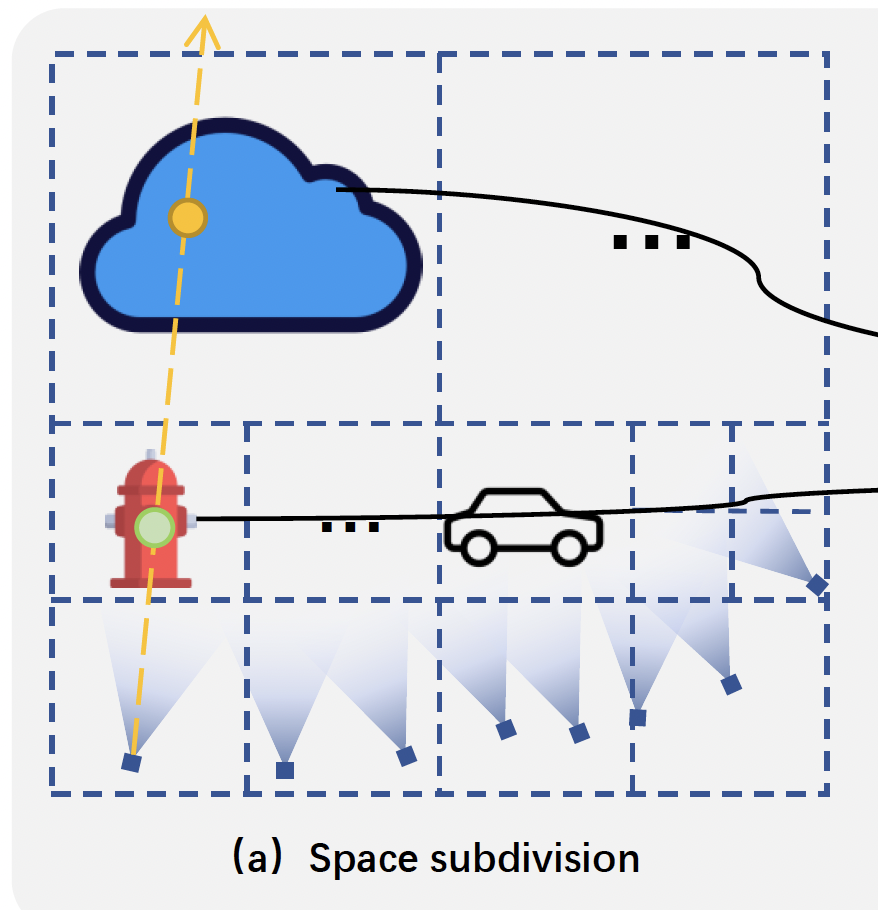
Space subdivision#

前面提到,由於 proper perspective warping 是否 proper 是 local property (區域的特性),因此需要將整個場景分割成不同的區域,使同個區域可以使用相同的 $F(\mathbf{x})$。
本篇使用 Octree data structure 來儲存 subdivided regions。
使用一個很大的 bounding box 作為 root node。約為所有 camera centers 的 512 倍大,使其能夠包含遠處的物體。
如果有任何可見相機的 camera center 到 node center 的距離 $d \le \lambda_s$,這個 node 將會被劃分成 8 個 child nodes (邊長為上一級的一半)。
$\lambda$ is preset to 3
如果當前 node 足夠小,則將其標記為 leaf node。否則持續檢查距離並重複這個過程直到有 $n_l$ 個 leaf nodes $\{S_i|i=1, 2, \ldots, n_l\}$。
- 每個 leaf node 都是一個 region $S$
- 若該區域可以被多於 $n_c=4$ 台相機看到,將會進一步希望選擇的 $n_c$ 台相機能夠使 the minimal pair-wise distance of the selected cameras 盡可能的大。
Scene representation#
- 如果為每個 warp space 都構建一個 grid representation,那將會有 $n_l$ 個 grid representation。
- 為了限制參數量,作者假設所有的 warping functions 會將不同的 leaf nodes 映射到相同的 warp space,並使用 multiple hash functions 在這個 warp space 上構建一個 hash-grid representation。
Hash grid with multiple hash functions#
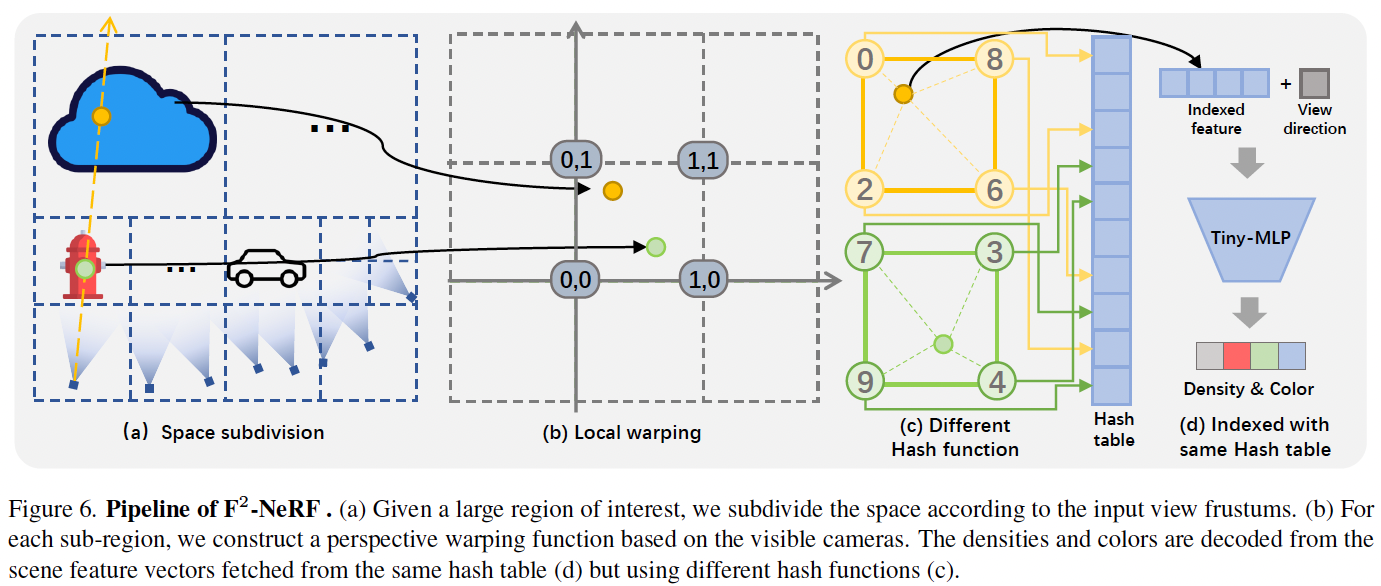
- 對不同的 leaf nodes 使用不同的 hash functions。
將 $i$-th leaf node 中的點 $\mathbf{x}$ 映射到 warp space (a to b)
$$ \mathbf{z} = F_i(\mathbf{x}) $$找到 $\mathbf{z}$ 的 8 個鄰近頂點 $\hat{\mathbf{v}}$ 。 (c 左)
為每個頂點計算 hash value。(c 右)
$$ \begin{align*} \text{Hash}_{i}(\hat{\mathbf{v}}) = \left( \bigoplus_{k=1}^{3} \hat{\mathbf{v}}_{k} \pi_{i,k} + \Delta_{i,k} \right) \mod L \end{align*}\tag{2} $$符號 描述 $\hat{\mathbf{v}}$ 鄰近的網格頂點 $i$ leaf node 的索引 $\oplus$ 位元異或運算 $\{ \pi_{i,k} \}$ 與 $\{ \Delta_{i,k} \}$ 固定在特定 leaf node 的隨機大質數 $k=1,2,3$ warp space 中 $x、y、z$ 座標的索引 $L$ 雜湊表的長度 從八個頂點的 feature vector 中插值出該點的 feature vector。(c 左)
最後將該點的 feature vector 與 view direction 餵入一個 tiny MLP 中生成 color and density。(d)
Perspective sampling#
由於 warping function 的定義是:warp space 中兩點之間的距離等於 image plane 上兩個投影點之間的距離和,因此若在 warp space 中進行均勻採樣:
- 歐式空間中並非均勻採樣。
- 但在圖像上近似於均勻採樣。
考慮一個 sample point $\mathbf{x}_i = \mathbf{o} + t_i \mathbf{d}$
$$ \mathbf{x}_{i+1} = \mathbf{x}_i + \frac{l}{\lVert J_i \mathbf{d} \rVert_2} \mathbf{d} $$符號 描述 $J_i$ 在 $\mathbf{x}_i$ 評估的透視扭曲函數 $F$ 的 Jacobian matrix $l$ 控制採樣間隔的預設參數
Rendering with perspective warping#
- 準備階段
- 將原始空間依照相機的視錐體進行細分
- 為每個子區域根據選定的相機構建局部扭曲函數
- 實際渲染階段
- 在相機光線上進行採樣
- 由多解析度雜湊網格產生取樣後的密度與顏色
- 對取樣的顏色進行加權累積
Training Loss#
$$ \begin{align*} \mathcal{L} = \mathcal{L}_{recon(c(r),c_{\text{gt}})} + \lambda_{\text{Disp}} \mathcal{L}_{\text{Disp}} + \lambda_{\text{TV}} \mathcal{L}_{\text{TV}} \end{align*}\tag{3} $$- Color reconstruction loss $$ \mathcal{L}_{recon}(c(r), c_{\text{gt}}) = \sqrt{(c(r) - c_{\text{gt}})^2 + \epsilon} $$
- Disparity loss $\mathcal{L}_{\text{Disp}}$
鼓勵視差(倒深度)不要過大,有助於減少漂浮偽影 - Total variance loss $L_{\text{TV}}$
鼓勵相鄰八分樹節點邊界的點具有相似的密度與顏色
Experiments#
Setting#
Datasets
- LLFF
- NeRF-360-V2
- Free dataset
包含 7 個場景
路徑狹長,且有多個聚焦的前景對象
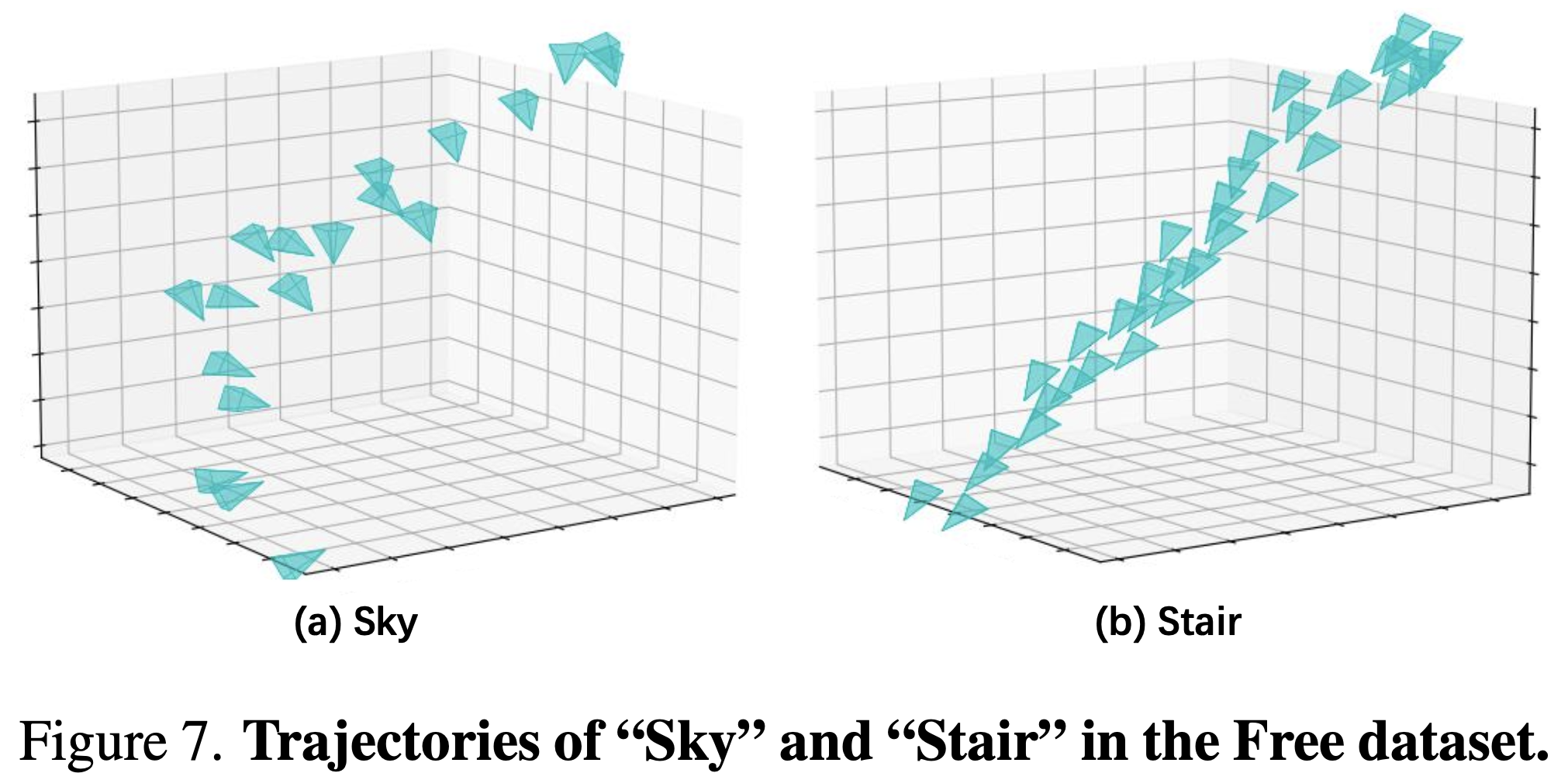
Metrics
- PSNR, SSIM, $\text{LPIPS}_{\text{VGG}}$
Baseline
- Voxel-based: DVGO, Plenoxels
- Hash-grid based: Instant-NGP
- MLP-based: NeRF++, mip-NeRF, mip-NeRF-360
Warping function
- LLFF:所有基線方法都使用 NDC warping function
- Free dataset 和 NeRF-360-V2
- Instant-NGP:官方實作
- 其他方法:使用 inverse sphere warping function
- $\text{F}^2$-NeRF 在所有資料集上皆使用 perspective warping function
Free Dataset#
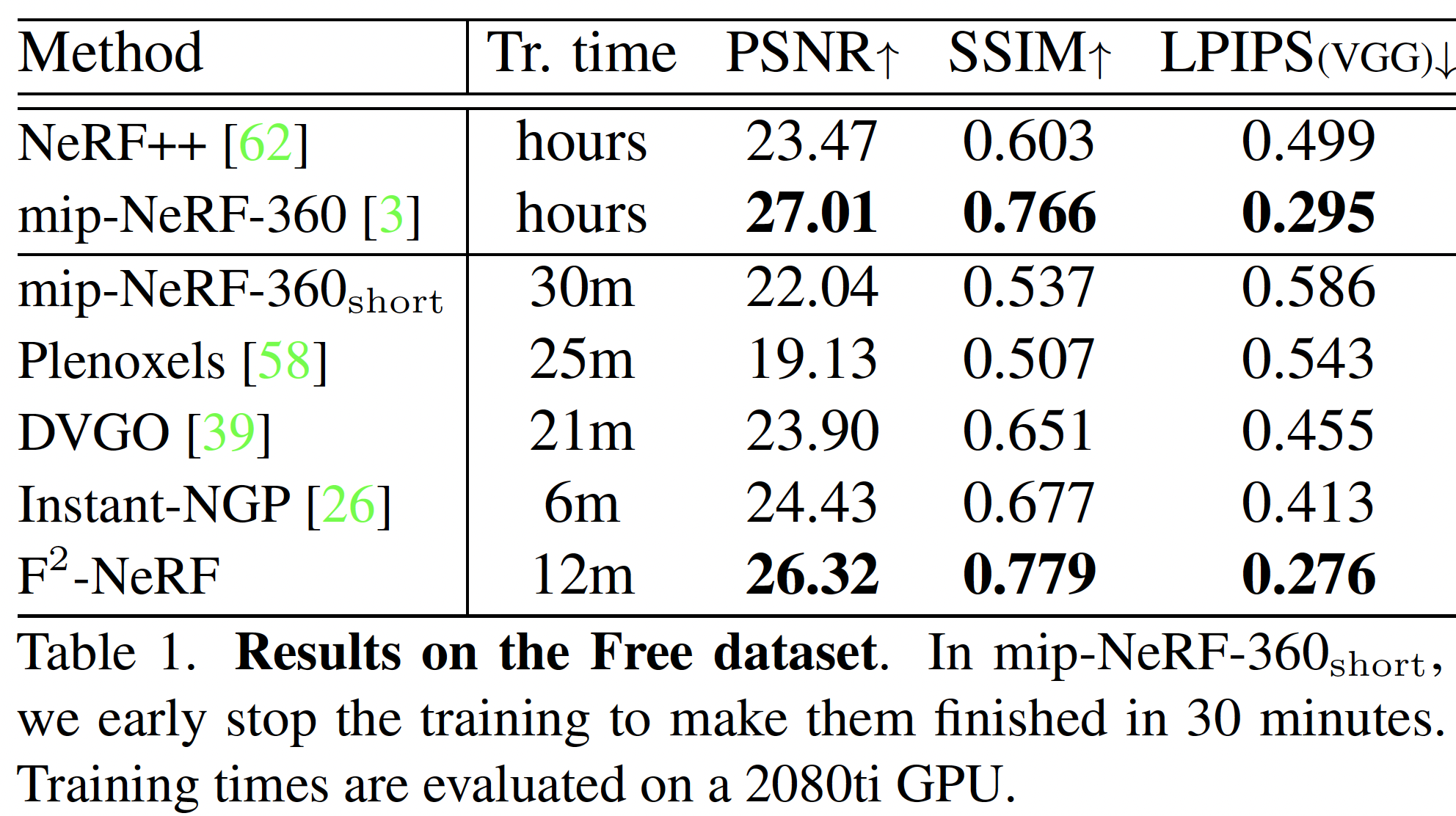

- 發現在 Free 數據集上⻑時間訓練 mip-NeRF-360 也能夠渲染出清晰的圖像。原因是在訓練過程中,mip-NeRF-360 使⽤的⼤型 MLP 網絡能夠逐漸將注意⼒集中在前景物體上,並⾃適應地為這些前景物體分配更多的容量。
NeRF-360-V2 Dataset#
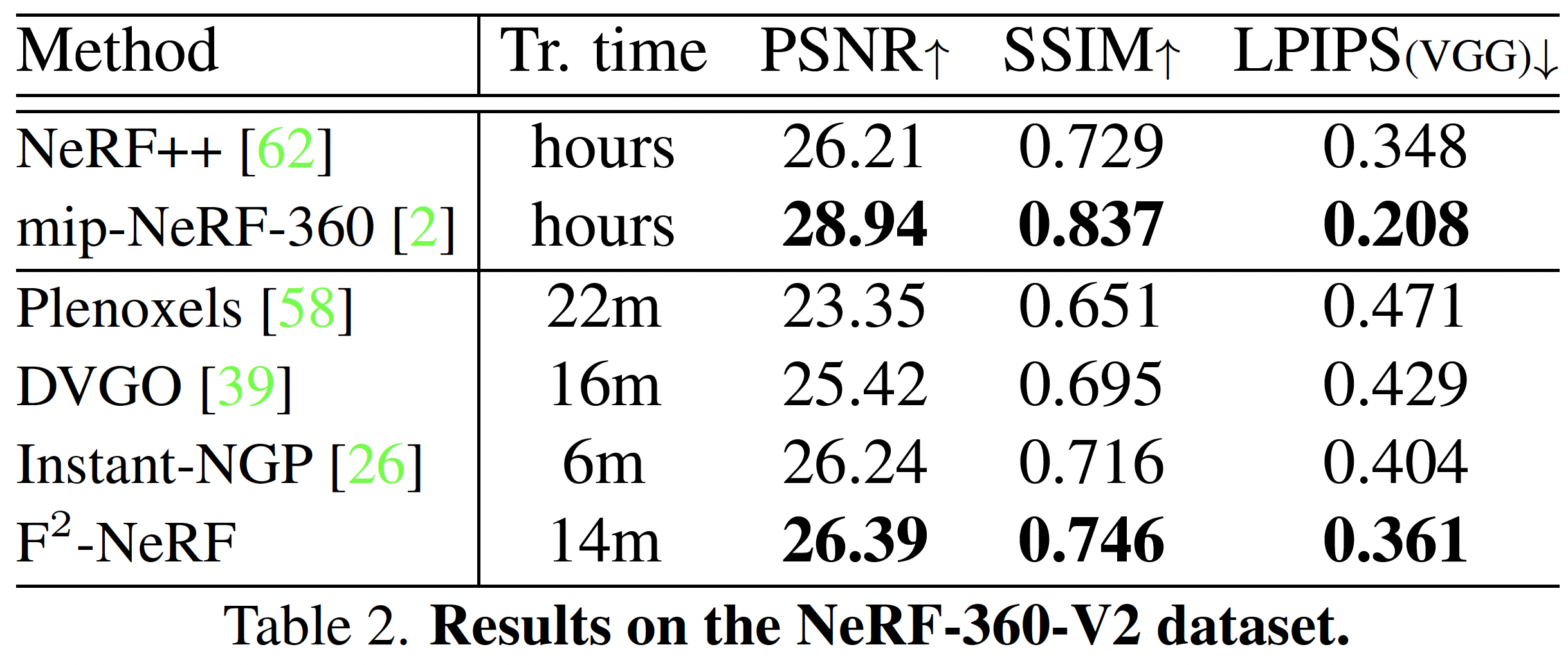
LLFF Dataset#
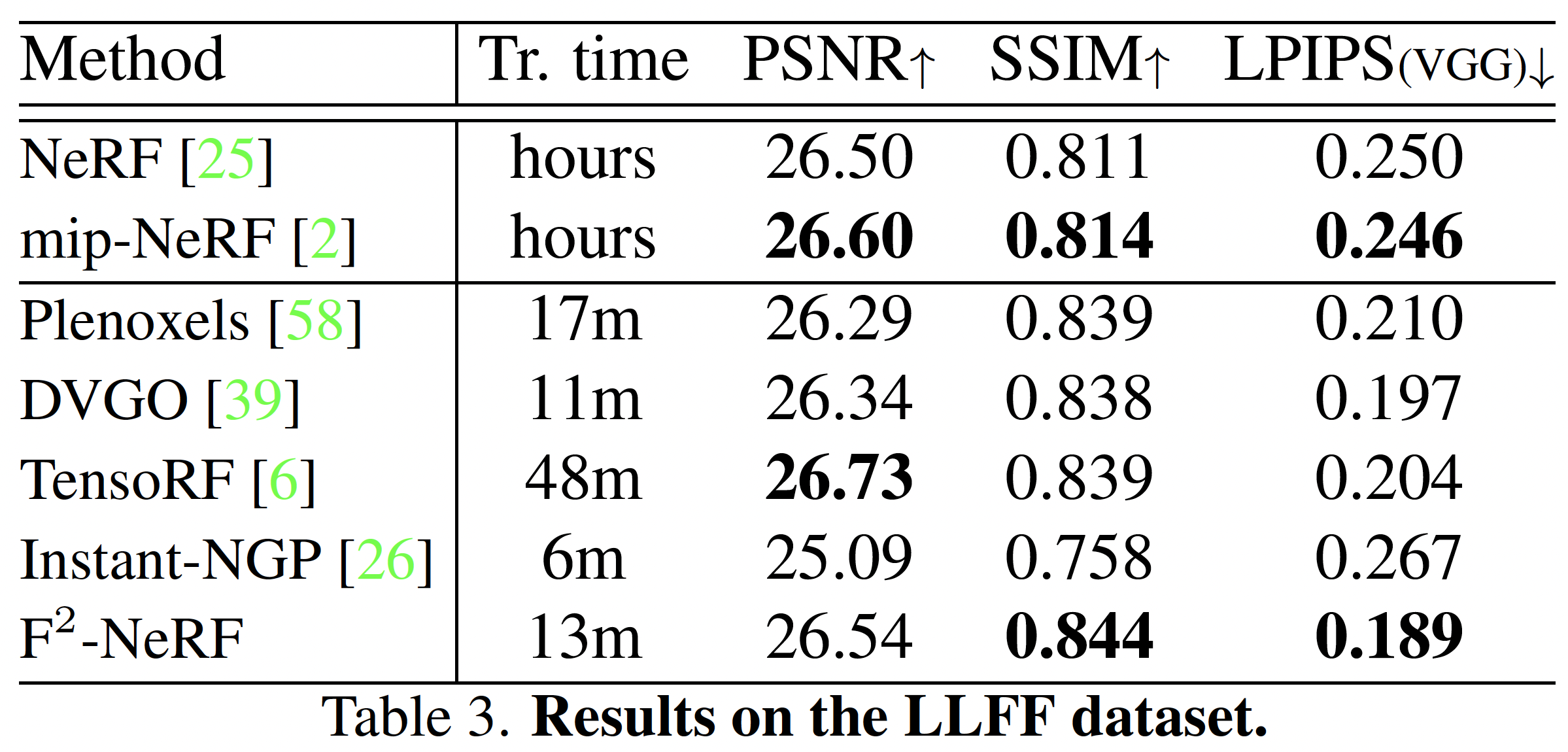
- 三種 datasets 的結果證明了 perspective warping 與不同軌跡的兼容。
Ablation Study#
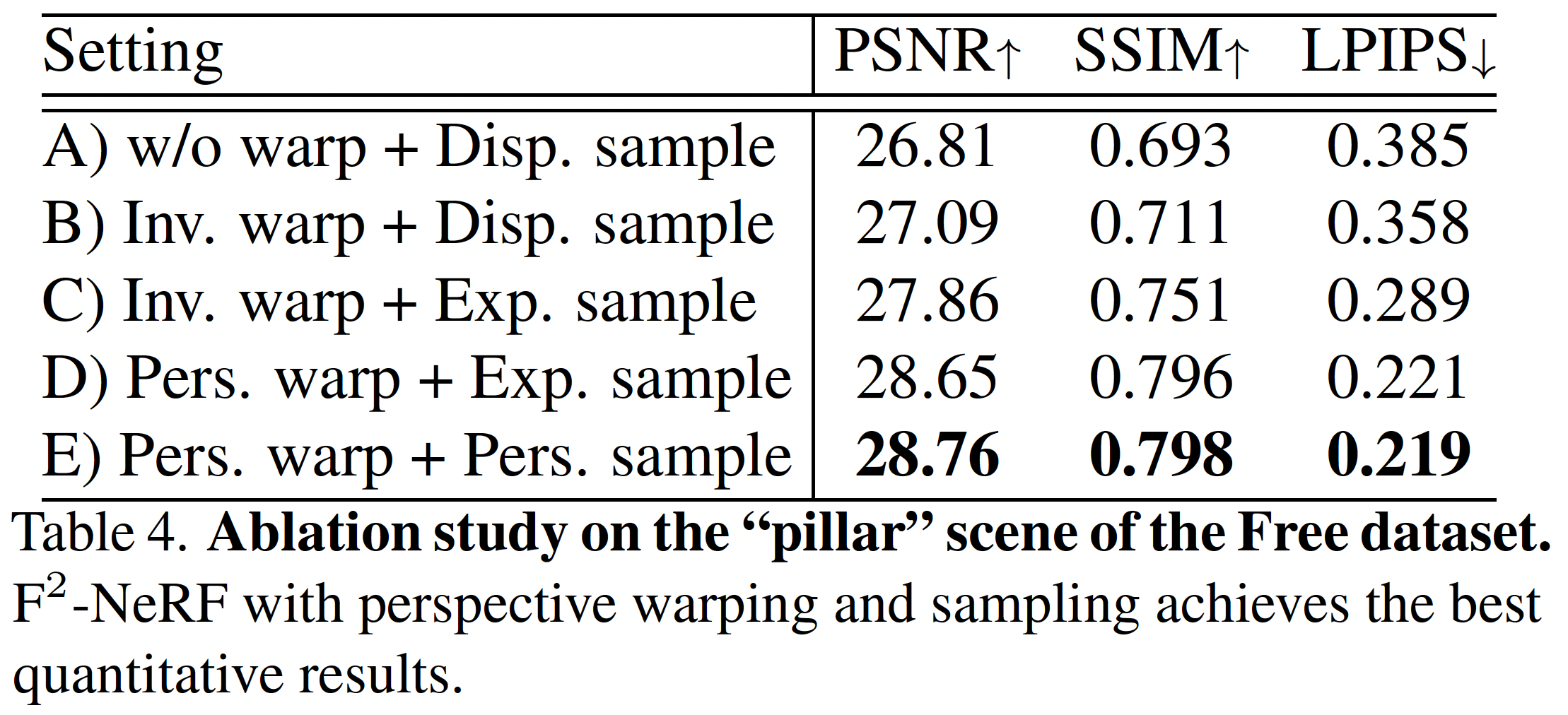

- 比較不同扭曲方式
- 無扭曲(w/o warp)
- inverse sphere warping(Inv. warp)
- perspective warping(Pers. warp)
- 比較不同採樣策略
- 由視差(倒深度)採樣(Disp. Sampling),使用於 NeRF-360
- 由指數函數採樣(Exp. Sampling),使用於 Instant-NGP
- perspective sampling(Pers. sample)
Conclusion#
- 提出 $\text{F}^2$-NeRF(Fast-Free-NeRF),第一個能夠處理大型無界場景自由相機軌跡的快速 NeRF 訓練方法
- 發展一個稱為 perspective warping 的通用空間扭曲方案,適用於任意相機軌跡
- 提出一個 空間細分演算法,自適應地對背景區域使用粗網格,並對前景區域使用細網格
