論文筆記 - 3DGS-Avatar: Animatable Avatars via Deformable 3D Gaussian Splatting

本篇筆記整理了 3DGS-Avatar (CVPR 2024) 的研究內容。該論文旨在解決從單眼視角影片（monocular video）高效重建可動畫（animatable）的著裝虛擬人像（clothed human avatars）的挑戰，特別是針對現有基於 NeRF 方法在訓練和渲染速度上的限制。筆記內容涵蓋了其核心方法：利用 3D Gaussian Splatting (3DGS) 作為基礎表示，設計了從標準空間（canonical space）到觀察空間（observation space）的變形流程，包括非剛性（non-rigid）和剛性（rigid）變形模組，以及一個用於處理視角相關顏色和局部變形的 Color MLP。此外，筆記也記錄了其優化策略，如姿態修正（pose correction）和關鍵的「盡可能等距」（as-isometric-as-possible, AIAP）正規化，以提升對未見姿態的泛化能力與重建品質。

論文資訊

• Link: https://arxiv.org/abs/2312.09228
• Conference: CVPR 2024

Introduction

#

• Research Background

  • 從影像中重建穿著衣服的虛擬人像（clothed human avatars）在電腦視覺領域中極具挑戰性，但在虛擬實境、遊戲及電子商務等領域具有重要應用價值。
  • 傳統方法通常需要密集、同步的多視角輸入，但這在現實場景中不切實際。
  • 隱式神經場（例如 Neural Radiance Fields, NeRFs）的進展，使從稀疏或單目錄像中高品質地重建穿衣人體的幾何結構和外觀成為可能。然而，這些方法計算量大且耗時，訓練需數天，推理需數秒。

• Limitation of Existing Works

  • 目前仍然沒有方法可以同時做到: 從單目錄像快速訓練，並支持即時推理以生成動畫虛擬人像。
  • 現有技術的高計算成本和長處理時間，限制了其在即時場景中的實際應用。

• Contributions

  • 本文提出了一種高效生成動畫虛擬人像的方法，具體來說：
    • 作者引入 3D Gaussian Splatting 技術來大幅提升人體重建的效率。
    • 他們開發了一種高效的變形網路，並結合了「盡可能等距」的正則化，以提升對未見姿勢配置的泛化能力。
    • 最終，本篇方法在渲染品質上與最先進方法相當甚至更優，同時在訓練時間和推理速度上實現了顯著的提升。

Methods

#

Preliminary - 3D Gaussian Splatting

#

• 基本流程：

  1. 首先，需要給定場景的點雲作為初始的位置資訊。
  2. 在初始化過程中，在點雲的位置上生成對應的 3D Gaussians，作為顯式的場景表示。
  3. 接著，根據相機的內外參數，將 3D Gaussian 投影到 2D 影像上，使 3D 結構能夠與2D觀測進行對應。
  4. 最後，通過針對 GPU 深度優化的 Tile Rasterizer，使用可微分的方式完成影像渲染，獲取最終的輸出影像。

• 與以往依賴隱式表達式（如 NeRF）的方法相比，3DGS 提升速度的關鍵在於以下三點：

  1. 顯式場景表示：
     • 3D Gaussians 是一種顯式的場景表示，省去了隱式表示中依賴大型神經網絡計算的複雜性，顯著減少了計算開銷。
  2. GPU 優化的 Tile Rasterizer：
     • 專為即時渲染設計的 Tile Rasterizer 深度優化了 GPU 的使用效率。
  3. 近似計算：
     • 針對 3D Gaussian 投影後的結果進行合理的近似，進一步降低了計算的複雜性。

• 隱藏的缺點：

  1. 使用 point cloud (3D Gaussian 的位置) 作為顯示表示，會大幅提升模型尺寸。
  2. 之前實驗的結果是，對於戶外的人，好像會產生與背景顏色相同顏色的 artifacts。

Pipeline

#

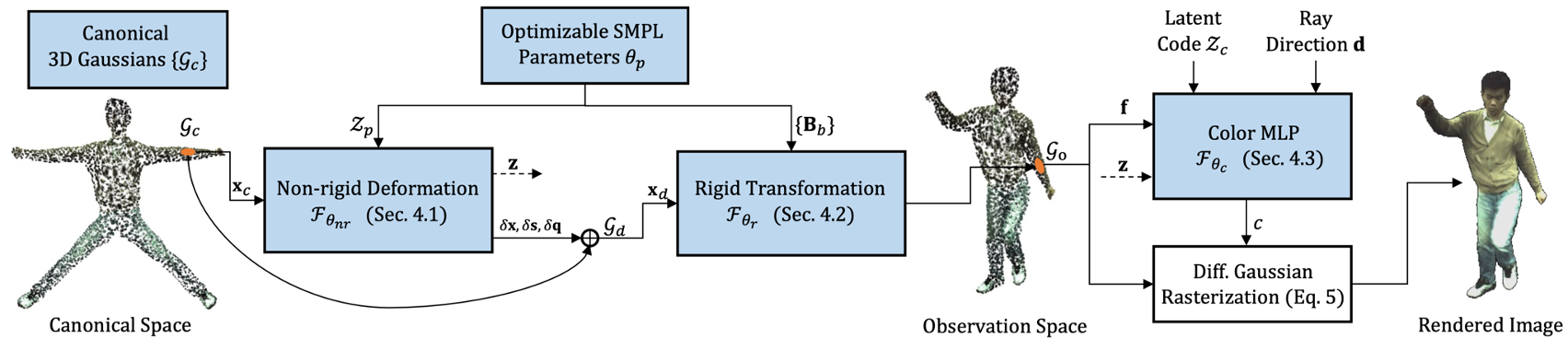
這個 3DGS-Avatar 從單目影像輸入開始，最終輸出可動畫的 3D 人物渲染圖像。

整體流程如圖 2 所示，主要分為以下幾步：

1. 3D Gaussians 初始化： 首先，在 Canonical Space 中，從 SMPL 骨架網格表面生成初始的 3D Gaussians，作為後續變形的基礎。
2. 映射到觀察空間： 接著，通過 non-rigid deformation module 和 rigid transformation module，將這些 3D Gaussians 根據姿態和形狀變形後，映射到 Observation Space。
3. 顏色建模： 隨後，利用 Color MLP 模組，結合高斯特徵、視角方向和潛在編碼，計算每個高斯點的顏色。
4. 影像渲染： 最後，透過可微分高斯光柵化技術，將這些 Gaussians 累積並渲染成最終影像。

Pose-dependent Non-rigid Deformation

#

Non-rigid Deformation Module 的目標是移除與姿勢相關的非剛性變形，如 Eq. 4 所示：

$$ \begin{equation} \{ \mathcal{G}_d \} = \mathcal{F}_{\theta_{nr}} \left( \{ \mathcal{G}_c \} ; \mathcal{Z}_p \right) \tag{4} \end{equation} $$

1. 對於每個 3D Gaussian，我們先將其座標通過多層雜湊網格來編碼，並與姿勢向量一同輸入至一個淺層MLP中，來預測高斯位置、尺度、旋轉的偏移量以及特徵向量。

   $$ \begin{align*} (\delta \mathbf{x}, \delta \mathbf{s}, \delta \mathbf{q}, \mathbf{z}) &= f_{\theta_{nr}} \left( \mathbf{x}_c; \mathcal{Z}_p \right), \tag{5} \end{align*} $$

2. delta x, s, q 用於計算變形後的位置、尺度以及旋轉，如Eq. 6-8 所示。

   $$ \begin{align*} \mathbf{x}_d &= \mathbf{x}_c + \delta \mathbf{x}, \tag{6} \\ \mathbf{s}_d &= \mathbf{s}_c \cdot \exp(\delta \mathbf{s}), \tag{7} \\ \mathbf{q}_d &= \mathbf{q}_c \cdot [1, \delta q_1, \delta q_2, \delta q_3]. \tag{8} \end{align*} $$

3. 特徵向量 $\mathbf{z}$ 則在後面的用於顏色的預測。

符號	描述
$\{ \mathcal{G} \}$	The 3D Gaussians.
$\mathcal{Z}_p$	A latent code which encodes SMPL pose and shape.
$\mathbf{x}$	The position of 3D Gaussian.
$\mathbf{s}$	The scaling factor of 3D Gaussian.
$\mathbf{q}$	The rotation quaternion of 3D Gaussian.
$\mathbf{z}$	A feature vector.

Rigid Transformation

#

Rigid Transformation Module 會進一步利用 LBS 將 3D Gaussians 根據輸入的人體姿勢，轉換至 Observation Space：

$$ \begin{align*} \{ \mathcal{G}_o \} &= \mathcal{F}_{\theta_r}\left( \{ \mathcal{G}_d \}; \{ \mathbf{B}_b \}_{b=1}^B \right) \tag{9} \\ \end{align*} $$

1. 對於每個 3D Gaussian ，我們會通過 Skinning MLP 預測其對應的 skinning weight，隨後根據 Eq. 10 計算其對應的轉換矩陣。

   $$ \begin{align*} \mathbf{T} &= \sum_{b=1}^B f_{\theta_r}(\mathbf{x}_d)_b \mathbf{B}_b \tag{10} \\ \end{align*} $$

2. 接著即能通過Eq.11, 12 將 3D Gaussian 轉換至 Observation Space。

   $$ \begin{align*} \mathbf{x}_o &= \mathbf{T} \mathbf{x}_d \tag{11} \\ \mathbf{R}_o &= \mathbf{T}_{1:3, 1:3} \mathbf{R}_d \tag{12} \end{align*} $$

符號	描述
$\{ \mathbf{B}_b \}_{b=1}^{\mathbf{B}}$	A set of rigid bone transformations.
$f_{\theta_{r}}$	The skinning MLP which predict skinning weights at the position $\mathbf{x}_d$.
$\mathbf{T}$	The transformation matrix of each 3D Gaussian.
$\mathbf{R}$	The rotation matrix.

Color MLP

#

• Limitations of 3DGS

  • 在 3DGS 中，作者利用 3D Gaussian 儲存於球面諧波係數來表現視角相關顏色，然而，對於單目輸入的任務而言，由於視角方向固定，導致測試時對未見視角的泛化能力差。
  • 另一方面，由於 3DGS 是針對靜態場景設計，因此並沒有考慮局部幾何變形對顏色的影響，比如衣服局部皺摺會造成自遮擋。

• 主要改進：

  • 首先，針對單目輸入的任務，作者使用 inverse rigid transformation 來標準化視角方向。

  • 接著，作者使用了一個 MLP 來增強顏色建模。該 MLP 以每個高斯的顏色特徵向量 $\mathbf{f}$、局部姿勢相關特徵向量 $\mathbf{z}$、每幀的潛在代碼 $\mathcal{Z}_c$ 以及使用標準化視角方向的三階球諧函數基底 $\gamma(\mathbf{\hat{d}})$ 來作為輸入，並預測 3D Gaussian 的顏色。

    $$ \begin{align*} c &= \mathcal{F}_{\theta_c}(\mathbf{f}, \mathbf{z}, \mathcal{Z}_c, \gamma(\hat{\mathbf{d}})) \tag{13} \end{align*} $$

    符號	描述
    $\mathbf{f}$	The per-Gaussian color feature vector.
    $\mathbf{z}$	The local pose-dependent feature vector.
    $\mathcal{Z}_c$	The per-frame latent code.
    $\gamma(\mathbf{\hat{d}})$	The third-degree spherical harmonics basis of the canonicalized viewing direction.

Optimization

#

Pose Correction

#

由於從影像中預測的 SMPL 參數可能不準確，因此作者在訓練過程中，持續優化姿勢參數。

1. 首先，將預測的每個序列的形體參數以及每幀的平移、全局旋轉和局部關節旋轉作為 $\theta_p$ 的初始值。
2. 接著，可以推導出骨骼轉換矩陣 $\{ \mathbf{B}_b \}$ 作為網路的輸入。
3. 最後，通過反向傳播直接進行最佳化。

As-isometric-as-possible Regularization

#

• Issue: 在處理來自單眼視頻的動態人體建模時，模型容易因輸入視角的稀疏性導致過度擬合，產生噪聲性的非剛性變形。

• Solution: 為解決此問題，作者引入 AIAP 正規化，以限制從標準空間到觀測空間的變形場，使其保持幾何一致性。

• 實作方法：

  • (Eq.14) 確保鄰近的 3D Gaussian 中心在變形前後的距離盡可能相等，從而維持相對位置的一致性。

    $$ \begin{align*} \mathcal{L}_{isopos} &= \sum_{i=1}^{N} \sum_{j \in \mathcal{N}_k(i)} \left| d(\mathbf{x}_c^{(i)}, \mathbf{x}_c^{(j)}) - d(\mathbf{x}_o^{(i)}, \mathbf{x}_o^{(j)}) \right| \tag{14} \\ \end{align*} $$

  • (Eq.15) 作者同時也約束了 Gaussian 斜方差矩陣變形前後的形狀變化。

    $$ \begin{align*} \mathcal{L}_{isocov} &= \sum_{i=1}^{N} \sum_{j \in \mathcal{N}_k(i)} \left| d(\Sigma_c^{(i)}, \Sigma_c^{(j)}) - d(\Sigma_o^{(i)}, \Sigma_o^{(j)}) \right| \tag{15} \end{align*} $$

  符號	描述
  $N$	The number of 3D Gaussians.
  $\mathcal{K}_k$	The k-nearest neighbourhood.
  $d(\cdot, \cdot)$	The distance function (L2-norm).

Loss Function

#

本篇的損失函數包括以下幾個組成部分：

• RGB loss: 用於約束 RGB ，由 $l1$ loss 和 perceptual loss (LPIPS) 組成。$l1$ loss 用於計算 pixel-wise 誤差，perceptual loss 提供對局部錯位的穩健性。

• Mask loss: 用於約束不透明度。

  • 不透明度 $O_p$ 的計算如下：

    $$ \begin{align*} O_p = \sum_i \alpha'_i \prod_{j=1}^{i-1} \left(1 - \alpha'_j\right) \end{align*} $$

  • 作者實驗發現使用 $l1$ loss 的收斂速度比 Binary Cross Entropy (BCE) loss 更快。

• Skinning loss: 作者在 canonical SMPL 網格表面上採樣 1024 個點 $\mathbf{X}_{skin}$，並且使用重心座標插值得到的對應蒙皮權重 $\mathbf{w}$ 對前向蒙皮網進行正規化。

  $$ \begin{align*} \mathcal{L}_{skin} = \frac{1}{\lvert \mathbf{X}_{skin} \rvert} \sum_{\mathbf{x}_{skin} \in \mathbf{X}_{skin}} \left\| f_{\theta_r}(\mathbf{x}_{skin}) - \mathbf{w} \right\|^2 \end{align*} $$

• As-isometric-as-possible loss: 分別對位置和協方差施加盡可能等距的正則化損失 $\mathcal{L}_{isopos}$ 和 $\mathcal{L}_{isocov}$。

最終，總損失如下：

$$ \begin{equation*} \begin{aligned} \mathcal{L} &= \lambda_{l1} \mathcal{L}_{l1} + \lambda_{perc} \mathcal{L}_{perc} + \lambda_{mask} \mathcal{L}_{mask} + \lambda_{skin} \mathcal{L}_{skin} \\ &\quad + \lambda_{isopos} \mathcal{L}_{isopos} + \lambda_{isocov} \mathcal{L}_{isocov} \end{aligned} \tag{16} \end{equation*} $$

Experiments

#

Experimental Setting

#

• Datasets

  • ZJU-Mocap
  • PeopleSnapshot

• Baselines

  • ZJU-Mocap: NeuralBody, HumanNeRF, MonoHuman 和 ARAH
  • Optimized ZJU-Mocap: Instant-NVR
  • PeopleSnapshot: InstantAvatar

• Metrics

  • PSNR
  • SSIM
  • LPIPS

Quantitative Results on ZJU-MoCap

#

• 該論文提出的方法在 PSNR 和 SSIM 指標上與 ARAH 方法表現相當，但在 LPIPS 指標上明顯優於所有基準方法。
• 同時，該方法在訓練速度和推理速度方面也顯示出顯著的提升，對於實際應用具有重要意義。
• 值得注意的是，Instant-NVR 是在針對 ZJU-MoCap 的優化數據上進行訓練和測試，因此作者未將其與其他基準方法直接比較。然而從結果來看，在大多數情況下，該方法的性能依然優於 Instant-NVR。

Qualitative Comparison on ZJU-MoCap

#

• Instant-NVR 生成的結果外觀過於平滑，且肢體部分容易出現嘈雜的偽影。

• ARAH 方法則出現明顯的幾何缺陷，例如身體穿孔的問題。

• HumanNeRF 可能存在不正確的身體結構，並伴隨較為明顯的偽影現象。

• 相比之下，本文提出的方法在綜合表現上更具優勢。雖然在部分案例中光線表現稍顯強烈，但整體外觀並無明顯的缺陷。

• 此外，作者還展示了新姿勢的合成結果，證明了該方法在處理新姿勢時的有效性。

Quantitative Results on PeopleSnapshot

#

• 本篇方法在 PSNR 和 LPIP S 的表現明顯優於 InstantAvatar。
• 同時在推理過程中速 度提高了 3 倍以上。

Qualitative Comparison on PeopleSnapshot

#

• 在 PeopleSnapshot 上的定性比較，差異較小。（論文內文認為更具細節，尤其是在臉部）

Ablation Study

#

• 在定量比較中，可以觀察到當移除不同模組後，LPIPS 指標顯示模型的性能有著相對應的下降。

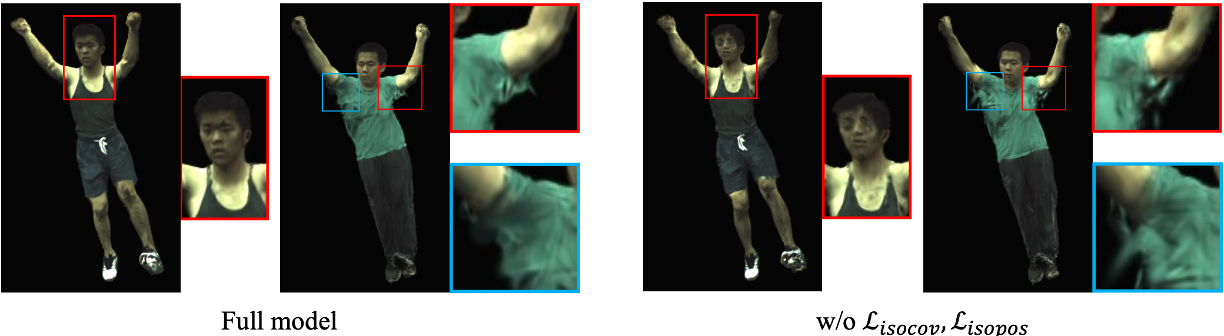
• 作者進一步對分布外的姿勢進行定性比較。
• 結果顯示盡可能等距的損失有助於約束 3D Gaussian 分佈在變形過程中遵循一致的運動，從而提高對新姿勢的泛化能力。

Conclusion

#

• 本文提出一種基於 3D Gaussian Splatting 的方法，能高效地從單目影片重建可動畫的穿衣人形。
• 作者利用非剛性變形模組、淺層 MLP 解碼顏色，並結合幾何正則化，顯著提升渲染品質與對新姿勢的泛化能力。
• 實驗結果顯示，相較於基線方法，該方法訓練速度提升 400 倍，推理速度提升 250 倍，且渲染質量更為優異。